一、插入排序
插入排序的思路:将数据列分成两组,一组是已排序的序列A,另一组是未排序的序列B。遍历B将B中的元素插入到A中,从而使序列有序。
1.1 直接插入排序
将序列分成两部分,从头到尾遍历序列完成排序。现在我们有:
- 序列L[0, n-1]
- 有序序列A[0, i-1]
- 无序序列B[i, n-1]
算法简述:
- 选择B的头部,顺序查找找到其在A中插入的位置k
- 将B插入到L[k];向后移动L[k, i-1],到L[k+1, i]。
- 重复直到遍历完数组
算法分析:
- 空间效率:复杂度O(1)
- 时间效率:在排序过程中,向A中指向了n-1次插入操作。在最好情况下,只用插入不用移动,时间复杂度为O(n);在最坏情况下,每次插入都移动i+1次,移动的总次数为:
。注意,这里下标i从1开始,数组的1号位置下标为0。在平均情况下,时间复杂度约为n2 / 4。因此其时间复杂度为O(n2)。 - 稳定性:因为是从后向前比较(或是反之),所以不用担心相同元素的相对位置发生变化,之间插入排序是一个稳定的排序算法。
- 适用性:顺序表、链表。
1.2 折半插入排序
和直接插入排序一样,只是查找的过程变为折半查找。
1.3 希尔排序
算法描述:
- 初始化 di = n / 2;
- 选取步长di,将序列分成间隔di的n/di组;
- 在组内进行插入排序;
- 令di+1 = di / 2;
- 重复(1, 4)步直到di == 1;
算法分析:
- 空间效率:复杂度O(1)。
- 时间效率:平均情况下为O(n1.3),最坏情况下为O(n2)
- 稳定性:分组的原因可能会改变相同元素的相对位置,其是不稳定的排序方法。
- 适用性:顺序表。
二、交换排序
2.1 冒泡排序
大部分人学习的第一个排序方法,按照排序准则将“最大/小”的元素放入序列的首部或末尾。
void BubbleSort(std::vector<ElementType>& Seq)
{
// i表示第i次排序,此时针对第i个元素,比较它和序列中剩下元素的大小,选出最小的放入第i个位置(交换ij的位置)
for (int i = 0; i < Seq.size(); ++i)
{
// 用于判断本次(i)是否发生了交换
bool flag { false };
for (int j = i; j < Seq.size(); ++j)
{
// 这里使用 < 作为排序准则
if (Seq[i] < Seq[j])
{
swap(Seq[i], Seq[j]);
flag = true;
}
}
// 如果没有发生交换,则说明序列已经有序
if (!flag) return;
}
return;
}
算法分析:
- 空间效率:swap需要使用一个中间变量,复杂度O(1)。
- 时间效率:当序列有序时,比较n-1次、移动0次,从而最好情况下的时间复杂度为O(n);当序列逆序时,比较:Sigmai=1n-1(n-i) = n(n-1) / 2、移动Sigmai=1n-13(n-i) = 3n(n-1) / 2,从而最坏情况下时间复杂度为O(n2)。
- 稳定性:不改变相同元素的相对位置,是稳定的排序方法。
2.2 快速排序
下面我们通过一个实例来说明,考虑序列:49、38、65、97、76、13、27、49。这里使用“<”作为排序准则。
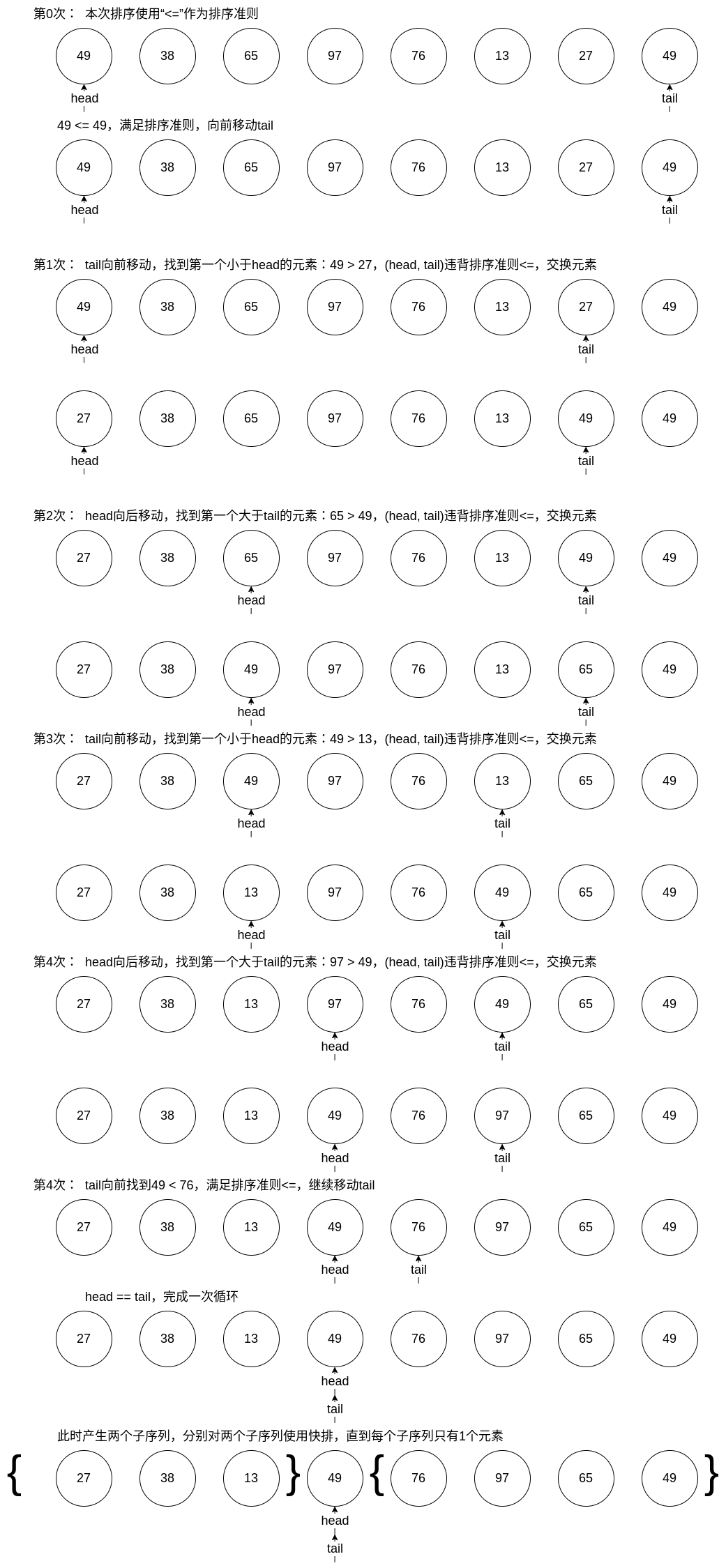
void QuickSort(std::vector<ElemType>& seq, int head, int tail)
{
if (head < tail) // 递归跳出条件
{
// 划分序列
int pos = Partition(seq, head, tail);
// 子序列快排
QuickSort(seq, head, pos - 1);
QuickSort(seq, pos + 1, tail);
}
}
// 序列分组
int Partition(std::vector<ElemType>& seq, int head, int tail)
{
OP op;
while (head < tail)
{
// 移动尾部指针,意图找到!(*head op *tail)
while (head < tail && op(seq[head], seq[tail])) --tail;
swap(seq[head], seq[tail]);
// 移动首部指针,意图找到!(*head op *tail)
while (head < tail && op(seq[head], seq[tail])) ++head;
swap(seq[head], seq[tail]);
}
return head;
}
// 排序准则,这里使用<=
class OP
{
public:
bool operator()(ElemType A, ElemType B)
{
return A <= B;
}
}
算法分析:
- 空间效率:递归需要借助一个工作栈完成,其容量与递归深度一致,最好情况下为O(log2n),最坏情况下为O(n-1),平均为O(log2n)。
- 时间效率:O(n2)。
- 稳定性:子序列以及排序准则(<或<=一类)的选择,其不稳定。
三、选择排序
3.1 简单选择排序
算法描述:
// 这里使用升序排序
void SelectSort(std::vector<ElemType> seq)
{
for (int i = 0; i < seq.size(); ++i)
{
// 选取最小元素的*位置*
ElemType minElePos = i;
for (int j = i + 1; j < seq.size(); ++j)
{
minElePos = (i < j) ?
i:
j;
}
if (minElePos != i) swap(seq[i], seq[minElePos]);
}
}
算法分析:
- 空间效率:swap消耗1个单位的中间变量,O(1)。
- 时间效率:O(n2)。
- 稳定性:不稳定。
3.2 堆排序
一个看着好像强无敌的排序方法,实际上没有那么强无敌,可能直接建立avl的效率更高。下面我们来看一下什么是堆、大根堆、小根堆。
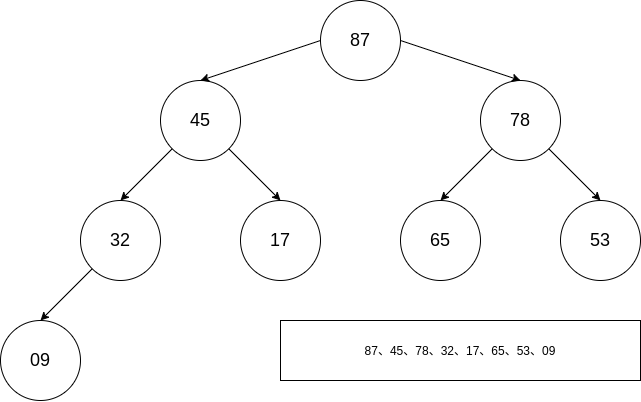
在上图中,L(i) >= max(L(2i), L(2i+1)),其是一个大根堆,也可以将该数组视为一个完全二叉树。大根堆的最大元素存放在堆顶,其任意非根节点的值小于其父节点。
堆排序的简单思路:
- 构造大根堆、小根堆
- 遍历,调整最大、最小元素到堆顶
- 移除堆顶元素,将最末元素移动到堆顶
- 重复直到堆中只有一个元素
下面我们通过一个实例来演示:
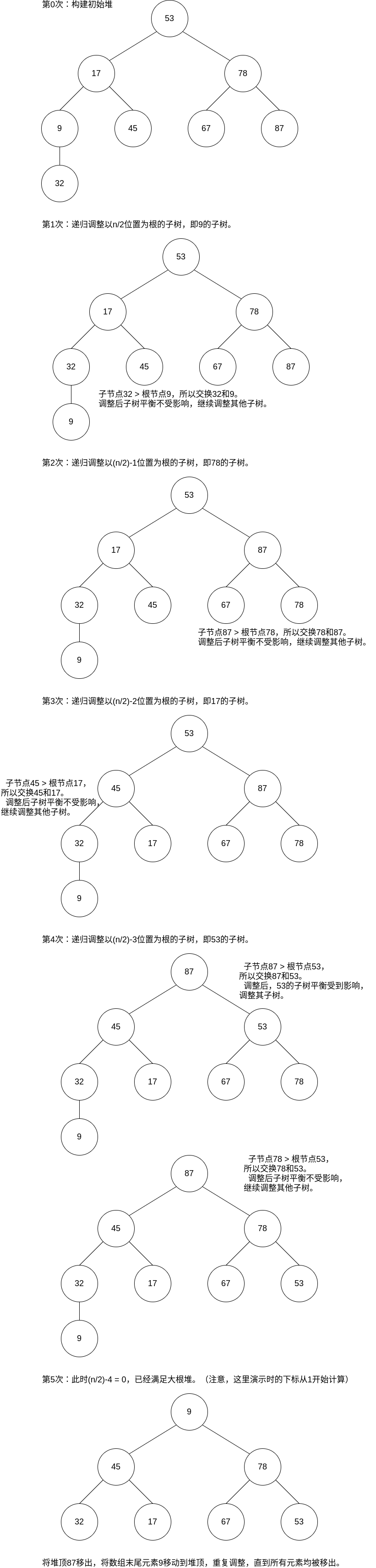
/* ===== 重复构造大根堆 ===== */
void BuildMaxHeap(std::vector<ElemType>& seq, int len)
{
// 下标范围[0, len-1]
for (int i = len / 2; i >= 0; --i)
{
HeadAdjust(seq, i, len);
}
}
/* ===== 节点移动 ===== */
void HeadAdjust(std::vector<ElemType>& seq, int rootK, int len)
{
// 对以rootK为根节点的子树进行调整
ElemType elemRootK = seq[rootK];
// 下标范围[0, len-1]
for (i = 2 * rootK; i < len; i *= 2)
{
// 选取更大的子节点,i或i+1
if (i < len && seq[i] < seq[i+1]) i++;
// 已经满足大根堆,跳出
if (elemRootK > seq[i])
{
break;
}
else
{
// 将i的值交给rootK,继续查看i的子树是否需要调整
seq[rootK] = seq[i];
rootK = i;
}
}
seq[rootK] = elemRootK;
}
/* ===== 堆排序 ===== */
void HeapSort(std::vector<ElemType>& seq)
{
BuildMaxHeap(seq, seq.size());
for (i = seq.size(); i > 0; --i)
{
// 移出堆顶seq[0]到堆底
swap(seq[i], seq[0]);
// 调整剩余的元素
HeadAdjust[seq, 0, i-1];
}
}
算法分析:
- 空间效率:O(1)。
- 时间效率:O(nlog2n)。
- 稳定性:不稳定。
四、并归排序和基数排序
4.1 并归排序
将数组分为n个列表,通过不断合并列表来实现排序,下面我们通过一个列子来演示:
/*
有序合并seq[low, mid-1]和seq[mid, high-1]
*/
void Merge(std::vector<ElemType>& seq, int low, int mid, int high)
{
// 用于存放seqLow和seqHigh的合并结果,最后写回到seq中
std::vector<ElemType> temp {seq};
for (int i{ low }, j{ high }, k{ 0 }
i < mid && j < high;
++k;)
{
seq[k] = (temp[i] < temp[j]) ?
temp[i++]:
temp[j++];
}
// 若seqL(tempL)未检测完,则全部拷贝入seq
while (i < mid) seq[k++] = temp[i++];
// 若seqH(tempH)未检测完,则全部拷贝入seq
while (j < high) seq[k++] = temp[j++];
}
void MergeSort((std::vector<ElemType>& seq, int low, int high)
{
if (low < high)
{
int mid = (low + high) / 2;
// 递归排序左子列
MergeSort(seq, low, mid);
// 递归排序右子列
MergeSort(seq, mid+1, high);
//合并
Merge(seq, low, high);
}
}
算法分析:
- 空间效率:O(n)。
- 时间效率:O(nlog2n)。
- 稳定性:稳定。
4.2 基数排序
看名字说得很抽象,下面我们来看一个实例:
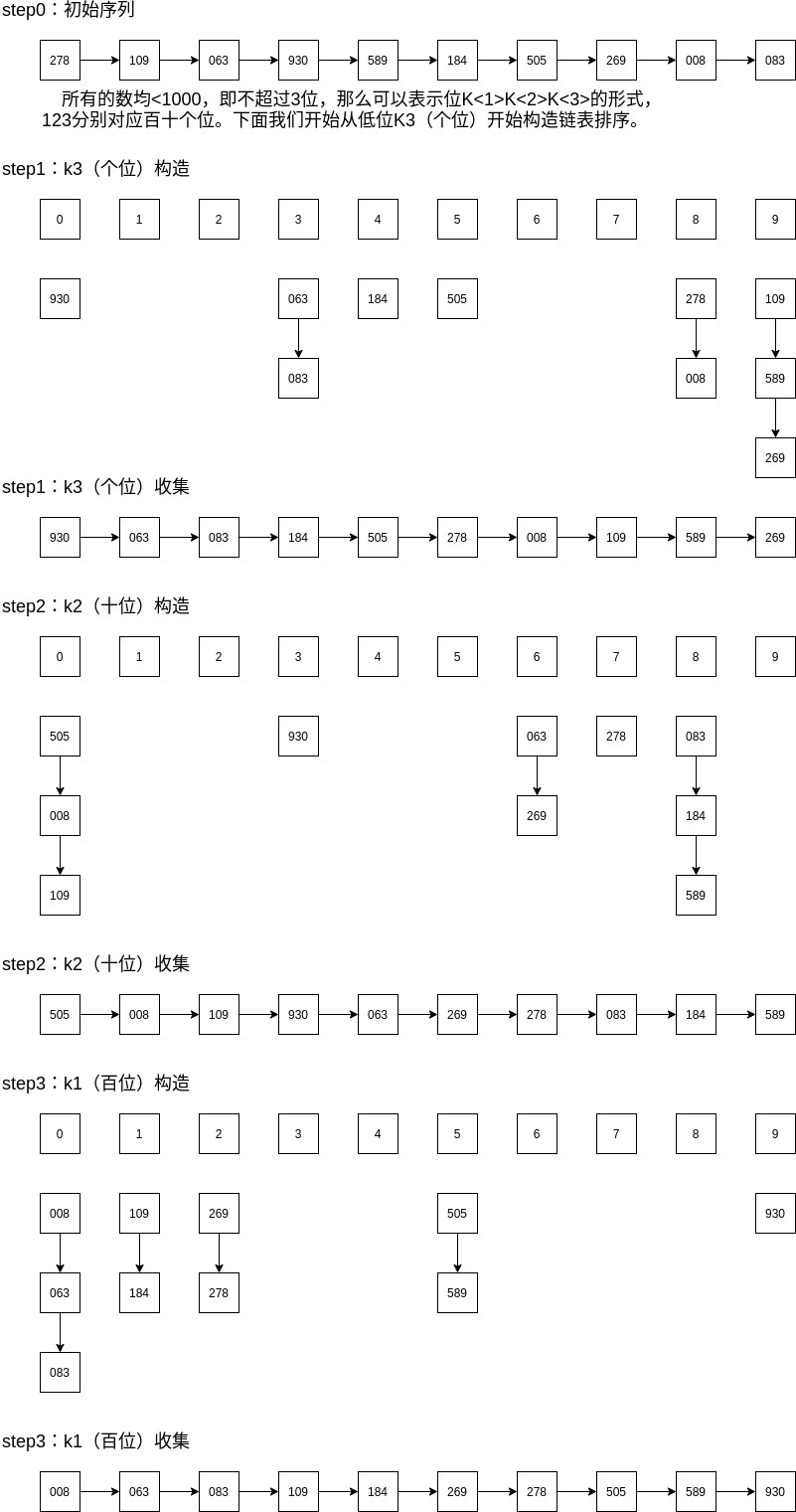
算法分析:
- 空间效率:O(r),r个队列的头、尾指针。
- 时间效率:O(d(n+r)),即d次分配+收集,每次分配构造使用n的时间,收回使用r的时间。
- 稳定性:稳定。





Comments | NOTHING