一、引言

  这里我们介绍Binary Search Tree的升级版，AVL。相比于BST，AVL要求了对于每个节点其左右子树的差至多为Limit（自己设定），这里的Limit一般选1（从0计算高度），即保证它是一颗平衡二叉树。
  AVL树的操作和BST基本一致，只需要在删除、插入返回前调用一次balance()，使得它从BST旋转为AVL。

• 完整项目：pgExamAvl

二、插入与删除

2.1 插入

template<typename elemType>
void Avl<elemType>::Insert(const elemType& ele, Node<elemType>*& node)
{
    // 有空位插
    if (!node)
    {
        node = new Node<elemType>(ele, nullptr, nullptr);
    }
    // 这个空位有人了，和他比较下，按一定排序准则选择左右，这里以 < 为排序准则。
    else if (ele < node->element)
    {
        this->Insert(ele, node->left);
    }
    else if (node->element < ele)
    {
        this->Insert(ele, node->right);
    }

    this->Balance(node);
}

2.2 删除

template<typename elemType>
void Avl<elemType>::Remove_val(const elemType& ele, Node<elemType>*& node)
{
    if (!node) return;

    // 不是目标，比较
    if (ele < node->element)
        this->Remove_val(ele, node->left);
    else if (ele > node->element)
        this->Remove_val(ele, node->left);
    // 找到目标
    else if (node->left && node->right)       // 被删除目标有两个节点
    {
        // 可替换左子树的最大值、右子树的最小值（中序向量的两个点，选一）
        node->element = this->FindMin(node->right)->element;
        // 更新删除目标
        Remove_val(node->element, node->right);
    }
    else                                    // 被删除目标只有一个节点或无节点
    {
        Node<elemType>* oldOne = node;
        node = (node->left) ?
            node->left :
            node->right;
        delete oldOne;
    }

    Balance(node);
}

三、旋转与平衡

3.1 旋转

  AVL的旋转可以分为两种，单旋和双选。对于左右子树的旋转其是对称的。

3.1.1 左子树单旋

Single Rotate with Left // LL
  现在我们有如下的一个二叉树，其节点violate是违反了AVL要求的节点，其高度更高的一边来自violate的左子树，我们称之为violateLeft。我们查看violateLeft的左右子树高度情况，发现violateLeft的左边比右边高，则其为LL情况，或称Single Rotate with Left。

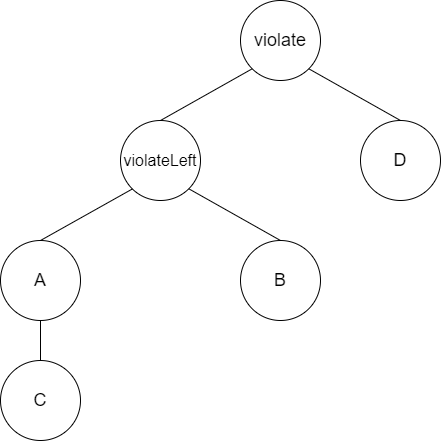
  变换操作：

1. violate->left = violateLeft->right;
2. violateLeft->right = violate;
3. violate = violateLeft; // 更新根节点

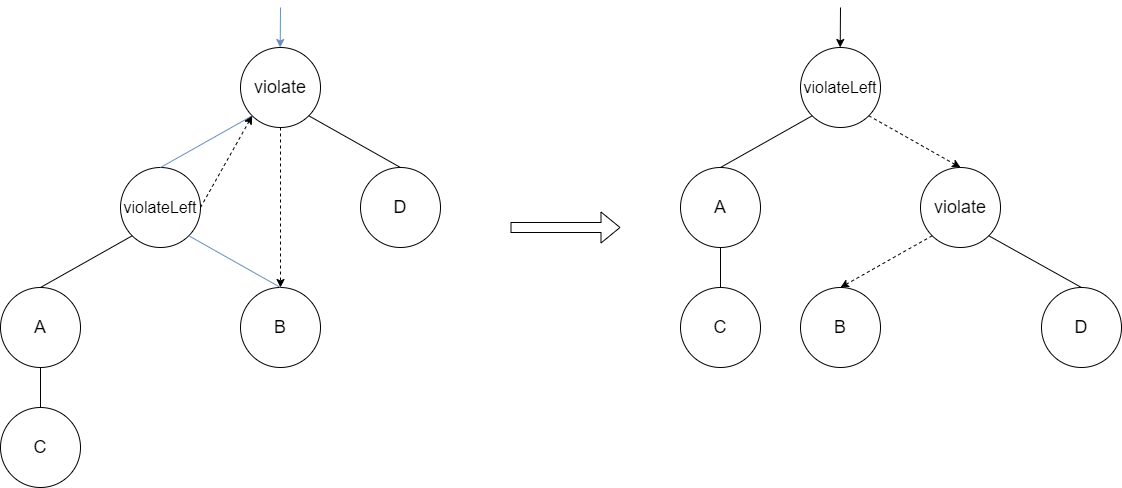
  RR的变换同理，下面是LL代码展示：

/* ===== Function 07 : LL ===== */
template<typename elemType>
void Avl<elemType>::LL(Node<elemType>*& violate)
{
    Node<elemType>* violateLeft = violate->left;

    // 交换节点
    violate->left = violateLeft->right;
    violateLeft->right = violate;

    // 高度更新
    violate->height = std::max(Height(violate->left), Height(violate->right)) + 1;
    violateLeft->height = std::max(Height(violateLeft->left), violate->height) + 1;

    violate = violateLeft;
}

3.1.2 左子树双旋

Double Rotate with Left // LR
  同样是上面的图，不过这次最高点来自violate->left->right，所以这是一次双旋。对于LR双旋，我们先对(voilate->left)使用RR单旋，再对(violate)使用LL单旋。

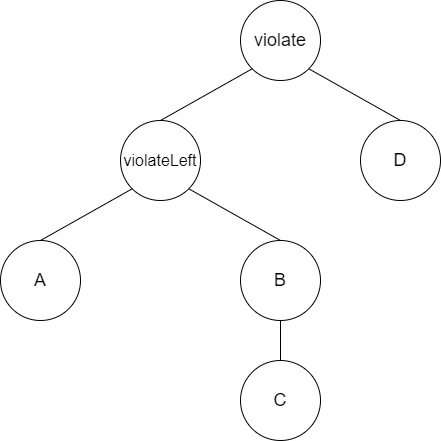
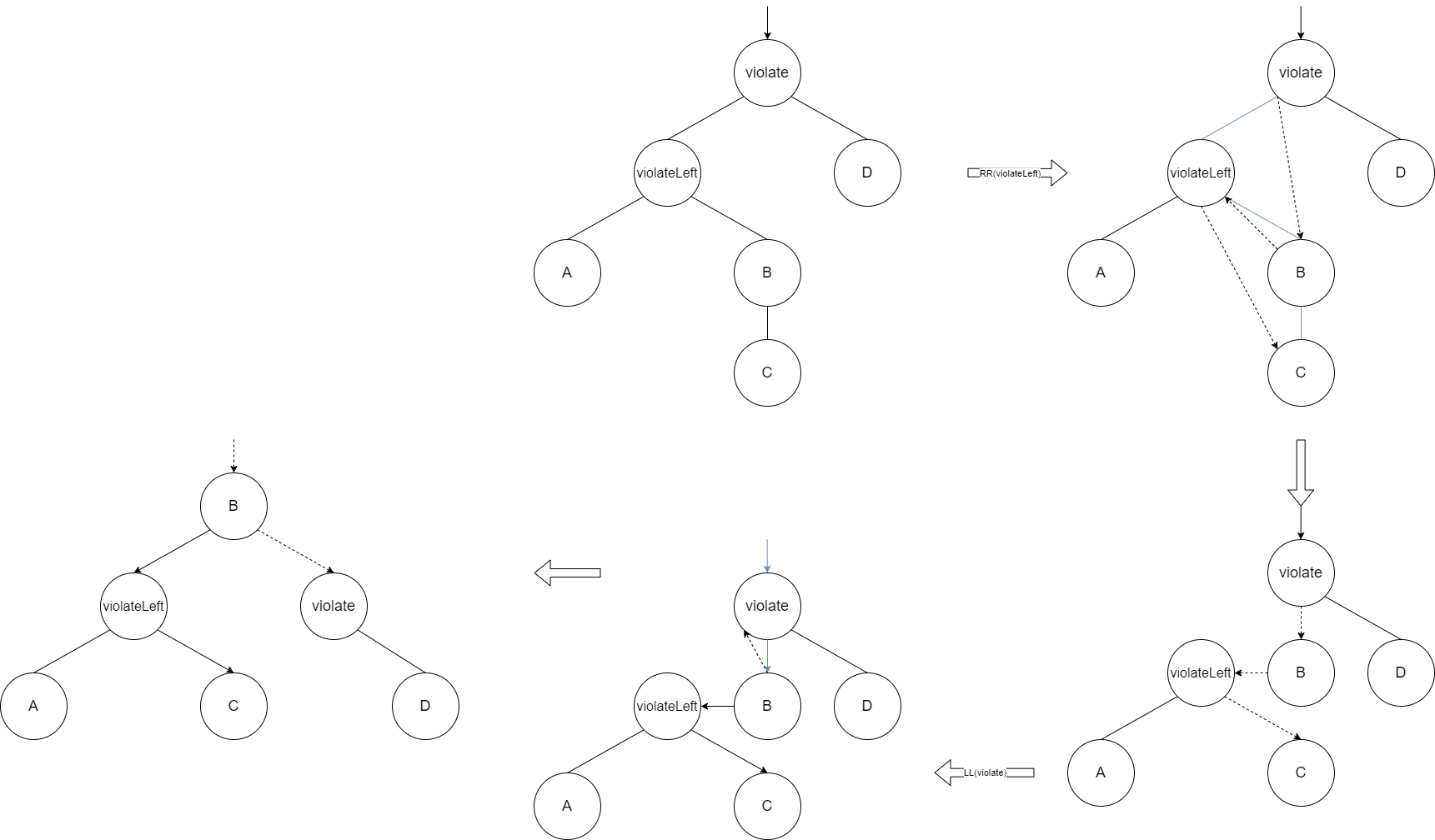
  变换操作：

1. RR(violate->left);
2. LL(violate);

  代码示例：

/* ===== Function 09 : LR ===== */
template<typename elemType>
void Avl<elemType>::LR(Node<elemType>*& violate)
{
    RR(violate->left);
    LL(violate);
}

3.2 平衡

  我们每执行一次插入、删除操作，就对当前节点执行一次balance()。
  判断方法如下，L表示当前节点的左子树，LL表示当前节点左子树的左子树。

1. L - R > 限制
   LL > LR
   LL();
   LL < LR
   LR();
2. R - L < 限制
   RR > RL
   RR();
   RR < RL
   RL();
3. 更新高度

  代码示例：

/* ===== Function 11 : 平衡 ===== */
template<typename elemType>
void Avl<elemType>::Balance(Node<elemType>*& node)
{
    if (!node)  return;

    // 左高
    if (Height(node->left) - Height(node->right) >= 2)
    {
        if (Height(node->left->left) >= Height(node->left->right))
        {
            LL(node);
        }
        else
        {
            LR(node);
        }
    }
    // 右高
    else if (Height(node->right) - Height(node->left) >= 2)
    {
        if (Height(node->right->right) >= Height(node->right->right))
        {
            RR(node);
        }
        else
        {
            RL(node);
        }
    }

    // 更新高度
    node->height = std::max(Height(node->left), Height(node->right)) + 1;
}