考虑这样一个问题：为r = (a|b)*abb构造一个DFA。
  对于正则表达式构造DFA的问题：第一步，为正则表达式构造一个NFA；第二步，由NFA转换为DFA表达式。

一、正则表达式构造NFA

参考：《编译原理》龙书，p102。

step 1: 由正则表达式构建语法树

  r = (a|b)*abb

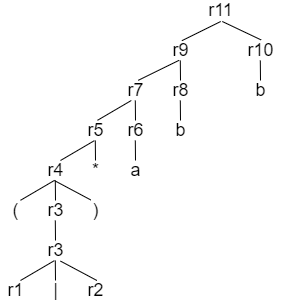
step 2: 为各子式构造NFA

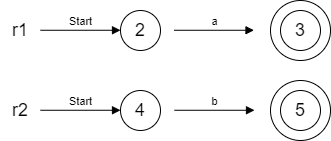
1.2.1 对于r1和r2构造NFA

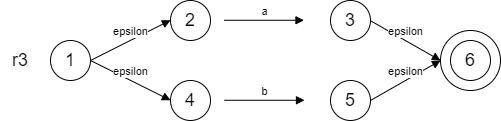
1.2.2 对r1和r2使用并运算得到r3

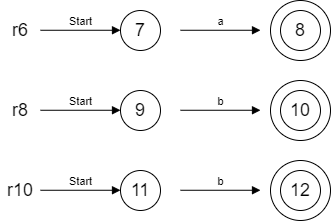
1.2.3 对r6、r8、r10构造NFA

1.2.4 对r6、r8、r10使用连接运算

1.2.5 连接2和4中的两部分

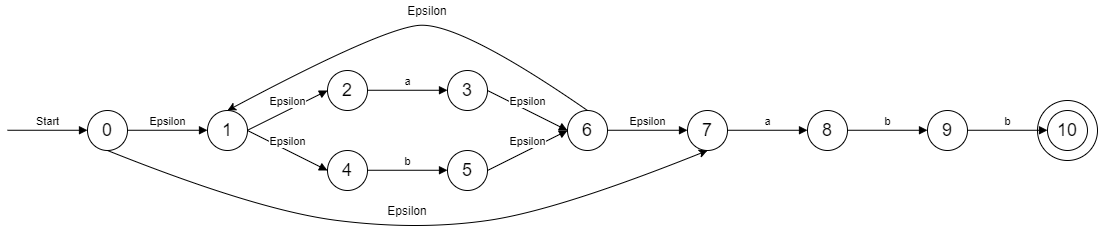
二、NFA构造DFA

  r = (a|b)*abb
  在第一节中，我们已经得到了r对应的NFA，下面我们通过NFA来构造DFA。

step 1: 求得start等价开始状态集合

    从状态0可以通过Epsilon到达的状态有{0, 1, 2, 4, 7}，这里包含了本身0状态，记作A = {0, 1, 2, 4, 7}，A为NFA的起始状态集合。

step 2: 寻找标记符号

    这里的输入有{a, b}两种，所以使用a和b来标记NFA状态集合。

step 3: 标记状态集合

2.3.1 使用{a, b}标记A

\begin{align}
Dtran[A, a] &= Epsilon-Closure(move(A, a))\newline
&= Epsilon-Closure({3, 8})\newline
&= {1, 2, 3, 4, 6, 7, 8} = B\newline
&B这里包含了本身{3, 8}状态，下同。
\end{align}

\begin{align}
Dtran[A, b] &= Epsilon-Closure(move(A, b))\newline
&= Epsilon-Closure({5})\newline
&= {1, 4, 5, 6, 7} = C
\end{align}
     Dtran[A, a]表示从DFA状态A可以到达的DFA状态。move(A, a)表示从状态A可以到达的点（NFA状态），本例中是{3, 8}。Epsilon-Closure({3, 8})在本例中表示从{3, 8}藉由a和Epsilon可以到达的点的集合。

2.3.2 使用{a, b}标记B、C

\begin{align}
Dtran[B, a] &= Epsilon-Closure(move(B, a))\newline
&= Epsilon-Closure({3, 8})\newline
&= {1, 2, 3, 4, 6, 7, 8} = B
\end{align}
\begin{align}
Dtran[B, b] &= Epsilon-Closure(move(B, b))\newline
&= Epsilon-Closure({5, 9})\newline
&= {1, 2, 4, 5, 6, 7, 9} = D
\end{align}
\begin{align}
Dtran[C, a] &= Epsilon-Closure(move(C, a))\newline
&= Epsilon-Closure({3, 8})\newline
&= {1, 2, 3, 4, 6, 7, 8} = B
\end{align}
\begin{align}
Dtran[C, b] &= Epsilon-Closure(move(C, b))\newline
&= Epsilon-Closure({5})\newline
&= {1, 4, 5, 6, 7} = C
\end{align}

2.3.3 使用{a, b}标记D

\begin{align}
Dtran[D, a] &= Epsilon-Closure(move(D, a))\newline
&= Epsilon-Closure({3, 8})\newline
&= {1, 2, 3, 4, 6, 7, 8} = B
\end{align}
\begin{align}
Dtran[D, b] &= Epsilon-Closure(move(D, b))\newline
&= Epsilon-Closure({5, 10})\newline
&= {1, 2, 4, 5, 6, 7, 10} = E
\end{align}

2.3.4 使用{a, b}标记E

\begin{align}
Dtran[E, a] &= Epsilon-Closure(move(E, a))\newline
&= Epsilon-Closure({3, 8})\newline
&= {1, 2, 3, 4, 6, 7, 8} = B
\end{align}
\begin{align}
Dtran[E, b] &= Epsilon-Closure(move(E, b))\newline
&= Epsilon-Closure({5})\newline
&= {1, 4, 5, 6, 7} = C
\end{align}

step 4: 状态全部被标记，可列表

NFA状态集合	DFA状态	通过a到达的DFA	通过b到达的DFA
{0, 1, 2, 4, 7}	A	B	C
{1, 2, 3, 4, 6, 7, 8}	B	B	D
{1, 4, 5, 6, 7}	C	B	C
{1, 2, 4, 5, 6, 7, 9}	D	B	E
{1, 2, 4, 5, 6, 7, 10}	E	B	C

step 5: 根据表画图

    我懒得画了。